[자료구조] 트리(Tree) 완벽 정리 : 개념부터 구현까지

참고 : GeeksForGeeks(https://www.geeksforgeeks.org/tree-data-structure/)

---

☑️ 트리(Tree) 완벽 정리 : 개념부터 구현까지

트리는 알고리즘 문제를 풀기 위해서 반드시 알아야 하는 자료구조 중 하나다. DFS, BFS 등 여러 알고리즘에서 트리가 나타나고 사용된다. 뿐만 아니라, 실제 상업 프로덕트에서도 트리 개념은 중요하게 사용된다. 기본적인 트리의 구조부터 여러가지 트리 개념에 대해서 알아보자.

 

먼저, 트리는 부모-자식 관계를 가지는 계층적 구조의 자료구조를 의미한다. 이름처럼 트리는 나무가 뿌리에서 시작해서 가지로 뻗어나가는 것처럼, 하나의 루트 노드에서 시작해서 여러 개의 자식 노드로 확장되는 구조를 가진다.

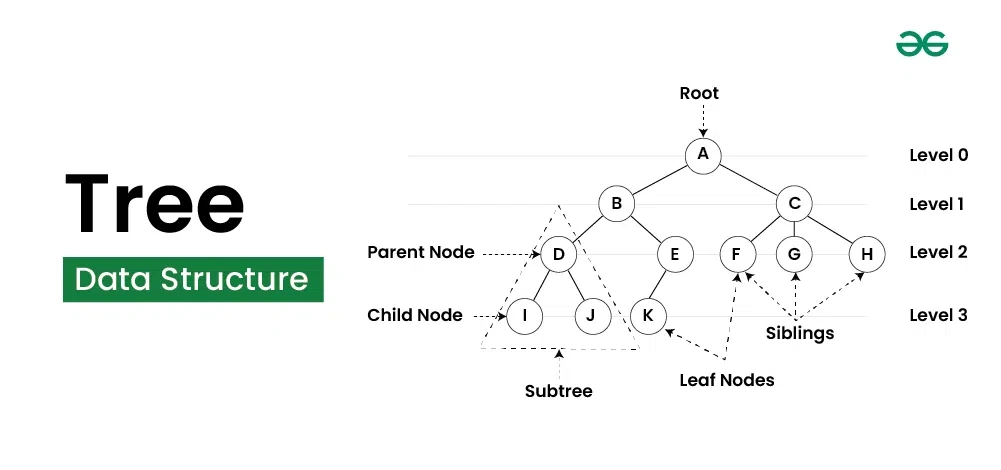
트리는 Node와 Edge로 연결되어 있다는 점에서 Graph와 비교하기도 하는데, 트리는 Graph에 속하는 자료구조다. 특징으로는 한 노드를 출발하고 다시 그 노드로 돌아오는 경로가 존재하지 않는다. 즉, 노드 순환이 없다는 특징을 가지고 있다.

 

1️⃣ 트리를 구성하는 용어들

트리는 자료구조를 사용하기 위해서 부르는 명칭들이 많다. 루트(Root) 노드, 부모(Parent) 노드, 자식(Child) 노드 등이 있는데, 용어를 보다시피, 우리가 실생활에 사용하는 단어들과 밀접해 있어서 외우는 것이 어렵지 않다.

 

📌 루트 노드(Root Node)

부모가 존재하지 않는 최상위 노드를 의미한다.

 

📌 부모 노드(Parent Node)

자식이 존재하는 노드를 의미한다. A 노드가 B 노드를 자식으로 가지고 있다면, B 노드의 부모 노드는 A 노드다.

 

📌 자식 노드(Child Node)

부모가 존재하는 노드를 의미한다. B 노드의 부모가 A 노드라면, B 노드는 A 노드에게 자식 노드다.

 

📌 형제 노드(Siblings Node)

같은 부모 노드를 두고 있는 노드를 의미한다.

 

📌 리프 노드(Leaf Node)

자식이 없는 노드를 의미한다.

 

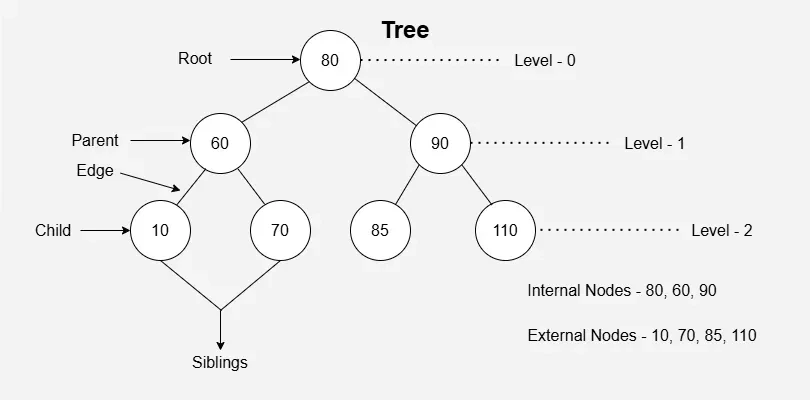
📌 내부 노드(Internal Node)

Leaf Node가 아닌 노드를 의미한다. (자식이 존재하는 노드들)

 

📌 노드 레벨(Node Level)

특정 깊이를 가지는 노드의 집합을 의미한다.

 

📌 높이(Height)

루트 노드를 1단계로 하위 노드로 내려가면서 1씩 확장한다. 루트 노드에서 얼마나 먼 거리에 있는지 판별할 때 사용된다.

 

📌 간선(Edge)

노드와 노드 사이를 잇는 선을 의미한다.

 

📌  서브트리(Subtree)

트리는 여러 서브트리로 분산될 수 있다. A 노드는 자식으로 B 노드와 C 노드를 가진다. 이 때, B 노드와 C 노드를 루트 노드로 변경하면 이들은 A 노드의 서브트리가 된다.

 

2️⃣ 가장 베이직한 트리(Tree) 코드

트리는 규칙 혹은 제약이 추가되면 이름이 붙으면서 다른 형태를 가지게 된다. 모든 트리 구조의 기본이 되는 트리의 코드는 다음과 같이 작성할 수 있다.

 

#include <iostream>
#include <vector>
#include <queue>

class TreeNode {
public:
    int data;
    std::vector<TreeNode*> children;
    
    TreeNode(int value) : data(value) {}
    
    void addChild(TreeNode* child) {
        children.push_back(child);
    }
    
    int getChildCount() const {
        return children.size();
    }
};

class Tree {
private:
    TreeNode* root;
    
    void preorderHelper(TreeNode* node, int depth = 0) {
        if (node == nullptr) return;
        
        for (int i = 0; i < depth; i++) {
            std::cout << "  ";
        }
        std::cout << node->data << std::endl;
        
        for (TreeNode* child : node->children) {
            preorderHelper(child, depth + 1);
        }
    }
    
    void deleteTree(TreeNode* node) {
        if (node == nullptr) return;
        
        for (TreeNode* child : node->children) {
            deleteTree(child);
        }
        
        delete node;
    }
    
    TreeNode* findHelper(TreeNode* node, int value) {
        if (node == nullptr) return nullptr;
        
        if (node->data == value) {
            return node;
        }
        
        for (TreeNode* child : node->children) {
            TreeNode* result = findHelper(child, value);
            if (result != nullptr) {
                return result;
            }
        }
        
        return nullptr;
    }

public:
    Tree() : root(nullptr) {}
    
    ~Tree() {
        deleteTree(root);
    }
    
    void setRoot(int value) {
        if (root != nullptr) {
            deleteTree(root);
        }
        root = new TreeNode(value);
    }
    
    TreeNode* getRoot() {
        return root;
    }
    
    void addNode(int parentValue, int childValue) {
        TreeNode* parent = findHelper(root, parentValue);
        if (parent != nullptr) {
            parent->addChild(new TreeNode(childValue));
        }
    }
    
    TreeNode* find(int value) {
        return findHelper(root, value);
    }
    
    void printTree() {
        if (root != nullptr) {
            preorderHelper(root);
        } else {
            std::cout << "Tree is empty" << std::endl;
        }
    }
    
    void levelOrder() {
        if (root == nullptr) return;
        
        std::queue<TreeNode*> q;
        q.push(root);
        
        while (!q.empty()) {
            TreeNode* current = q.front();
            q.pop();
            
            std::cout << current->data << " ";
            
            for (TreeNode* child : current->children) {
                q.push(child);
            }
        }
        std::cout << std::endl;
    }
    
    int getHeight(TreeNode* node) {
        if (node == nullptr) return -1;
        
        int maxHeight = -1;
        for (TreeNode* child : node->children) {
            int childHeight = getHeight(child);
            maxHeight = std::max(maxHeight, childHeight);
        }
        
        return maxHeight + 1;
    }
    
    int getTreeHeight() {
        return getHeight(root);
    }
};

int main() {
    Tree tree;
    
    tree.setRoot(1);
    tree.addNode(1, 2);
    tree.addNode(1, 3);
    tree.addNode(1, 4);
    tree.addNode(2, 5);
    tree.addNode(2, 6);
    tree.addNode(3, 7);
    tree.addNode(4, 8);
    tree.addNode(4, 9);
    tree.addNode(4, 10);
    
    std::cout << "Tree structure:" << std::endl;
    tree.printTree();
    
    std::cout << "\nLevel order traversal: ";
    tree.levelOrder();
    
    std::cout << "Tree height: " << tree.getTreeHeight() << std::endl;
    
    TreeNode* found = tree.find(7);
    if (found) {
        std::cout << "Found node: " << found->data << std::endl;
    }
    
    return 0;
}

 

3️⃣ 이외 : 다양한 트리 구조들

트리는 사용성이 쉬우며 효율성이 좋다. 그렇기 때문에 단순한 형태의 트리를 다양하게 바리에이션을 주어 트리의 종류가 꽤 많은 편인데, 그 중에서 유명한 트리들은 이진 트리(Binary Tree), 이진 검색 트리(Binary Search Tree), AVL 트리, 레드-블랙 트리, B 트리 등이 존재한다.

 

📌 이진 트리(Binary Tree)

각 노드가 최대 2개의 자식을 가지는 트리 구조.

 

📌 이진 검색 트리(Binary Search Treee)

이진 트리에 정렬 규칙을 추가한 트리로, 왼쪽 자식 노드는 부모 값보다 작으며, 오른쪽 자식 노드는 부모 값 보다 크다는 특징을 가진다. 성능이 보완되었으나, 한쪽으로 치우쳐진 편항된 트리의 모습을 가질 수 있다.

 

📌 AVL 트리

이진 검색 트리의 단점을 보완한 트리로, 모든 노드에서 왼쪽, 오른쪽 서브트리의 높이 차이가 최대 1이 되도록 균형을 맞춘다. 이런 특징을 가진 트리를 자가 균형 트리라고 한다.

 

📌 레드-블랙 트리(Red-Black Tree)

AVL 트리와 같이 자가 균형 트리로 스스로 편향된 트리를 방지한다. 노드에 색상(Red, Black)을 부여하고 규칙을 통해서 균형을 유지한다.

 

📌 B 트리

여러 개의 자식을 가질 수 있는 트리로 DB 혹은 파일 시스템에서 사용된다. 한 노드에 여러 개의 키를 저장할 수 있고 모든 리프 노드가 같은 레벨에 있어야 한다.