
01. A* 알고리즘이란?
A* 알고리즘은 경로 값과 휴리스틱 값을 사용해서 최단 경로를 탐색한다. Dijkstra 알고리즘의 단점을 보완하여 만들어진 알고리즘이며, 길을 찾기 위한 동작에서 대표적으로 사용되는 알고리즘이다.
탐색 공간인 Graph가 존재하며, 각 지점을 의미하는 Node와 지점을 서로 연결하는 Edge로 이루어지며, f(n) = g(n) + h(n) 공식을 따라서 최단 경로를 탐색한다.
02. 휴리스틱이란?
A* 알고리즘에서 휴리스틱 함수라고 불리우는 것은 컴퓨터 공학에서만 사용되는 것이 아니다. 기존 휴리스틱 이론을 컴퓨터 공학에서도 사용하는 것이다. 휴리스틱 이론은 경험에 기반하여 문제를 해결하는 것을 의미한다. 간단하게 설명하면 개인의 직관으로 판단하는 방법을 말한다.
03. 어떻게 휴리스틱이 A* 알고리즘에서 사용되는가?
f(n) = g(n) + h(n) 공식에서 h(n) 함수는 휴리스틱 함수를 의미한다. 해당하는 Node가 목표 지점의 Node까지 도달을 위해서 대략적으로 남은 거리를 가지고 있다. 어떻게 이런 '목표 지점까지 대략적인 거리'를 설정할 수 있을까? 대표적으로 맨하탄 거리, 유클리드 거리, 임의 부여가 있다.
A* 알고리즘에서 휴리스틱은 성능에 굉장히 영향을 많이 끼치기 때문에 조심스럽게 적절한 휴리스틱 함수를 대입해야만 한다.
04. A* 알고리즘의 작동 방식
A* 알고리즘은 탐색을 위해서 휴리스틱과 이동 Cost뿐만 아니라, Open Set과 Closed Set이 필요하다. Set이라고 불리우는 컨테이너들은 탐색할 Node의 정보를 가진다. Open Set은 가중치 계산이 끝나지 않은 Node에 대한 정보를 담으며, Closed Set은 가중치 계산이 끝나 방문할 필요가 없는 Node의 정보를 담는다.
아래 이미지를 통해서 구체적인 작동 방식을 보자. 아래 이미지에는 Node와 Edge로 이루어진 Graph가 존재한다. Start Node는 A이며, End Node는 E다. 파란색 글씨는 이동 코스트를 의미하며, 검정색 글씨는 휴리스틱 코스트를 의미한다.
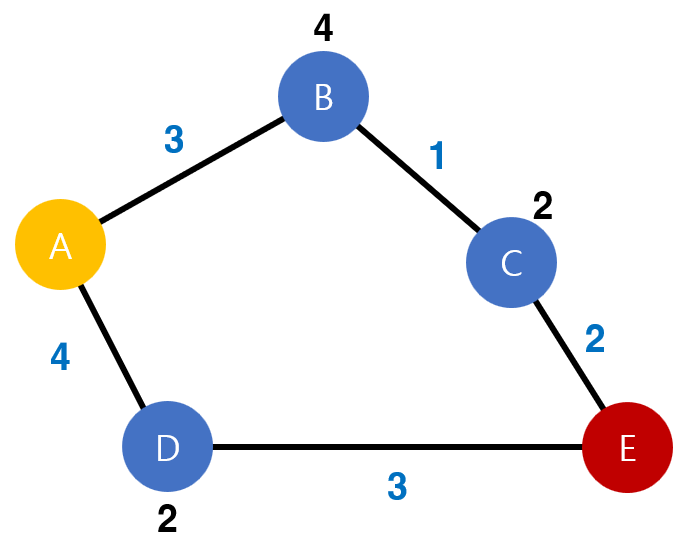
위 그래프를 탐색하기 위해서 A* 알고리즘은 다음과 같은 작업을 진행한다.
1. 시작 Node를 탐색하고 주변 Node 중에서 가장 작은 Cost를 가진 Node로 이동한다.
Node A ▶ Node B : Cost가 7 필요하다.
Node A ▶ Node D : Cost가 6 필요하다. ( 적은 값 )
2. 노드 D로 이동하고 주변 Node를 탐색한다.
이전 값보다 큰 Cost가 필요로 한다면, 이전 Node로 이동한다.
Node D ▶ Node E : Cost가 9 필요하다. ( 이전보다 높은 값이므로 이전 Node B로 이동한다. )
3. 1번과 2번을 반복하여 가장 작은 Cost의 Node를 찾는다. ( 가장 Cost가 작은 Node는 D다. )
4. 현재 위치한 Node가 End Node면 알고리즘을 종료한다.
05. Example Code - C#
using System;
using System.Collections.Generic;
class AStar
{
public class Node
{
public int X { get; set; }
public int Y { get; set; }
public int G { get; set; }
public int H { get; set; }
public Node Parent { get; set; }
public int F
{
get { return G + H; }
}
public Node(int x, int y)
{
X = x;
Y = y;
}
}
private static List<Node> GetNeighbors(Node node, int[,] grid)
{
List<Node> neighbors = new List<Node>();
int[] dx = { -1, 1, 0, 0 };
int[] dy = { 0, 0, -1, 1 };
for (int i = 0; i < 4; i++)
{
int nx = node.X + dx[i];
int ny = node.Y + dy[i];
if (nx >= 0 && ny >= 0 && nx < grid.GetLength(0) && ny < grid.GetLength(1) && grid[nx, ny] == 0)
{
neighbors.Add(new Node(nx, ny));
}
}
return neighbors;
}
private static int Heuristic(Node a, Node b)
{
return Math.Abs(a.X - b.X) + Math.Abs(a.Y - b.Y);
}
public static List<Node> FindPath(int[,] grid, Node start, Node goal)
{
List<Node> openList = new List<Node>();
HashSet<Node> closedList = new HashSet<Node>();
start.G = 0;
start.H = Heuristic(start, goal);
openList.Add(start);
while (openList.Count > 0)
{
openList.Sort((a, b) => a.F.CompareTo(b.F));
Node current = openList[0];
if (current.X == goal.X && current.Y == goal.Y)
{
List<Node> path = new List<Node>();
while (current != null)
{
path.Add(current);
current = current.Parent;
}
path.Reverse();
return path;
}
openList.Remove(current);
closedList.Add(current);
foreach (Node neighbor in GetNeighbors(current, grid))
{
if (closedList.Contains(neighbor))
{
continue;
}
int tentativeG = current.G + 1;
if (!openList.Contains(neighbor) || tentativeG < neighbor.G)
{
neighbor.Parent = current;
neighbor.G = tentativeG;
neighbor.H = Heuristic(neighbor, goal);
if (!openList.Contains(neighbor))
{
openList.Add(neighbor);
}
}
}
}
return null; // 경로를 찾을 수 없는 경우
}
static void Main(string[] args)
{
int[,] grid = {
{ 0, 1, 0, 0, 0 },
{ 0, 1, 0, 1, 0 },
{ 0, 0, 0, 1, 0 },
{ 0, 1, 0, 0, 0 },
{ 0, 0, 0, 1, 0 }
};
Node start = new Node(0, 0);
Node goal = new Node(4, 4);
List<Node> path = FindPath(grid, start, goal);
if (path != null)
{
foreach (Node node in path)
{
Console.WriteLine($"({node.X}, {node.Y})");
}
}
else
{
Console.WriteLine("경로를 찾을 수 없습니다.");
}
}
}출처 1 : 이득우의 꼭 배워야하는 게임 알고리즘 https://www.inflearn.com/course/%EA%B2%8C%EC%9E%84-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98/
출처 2 : A* 알고리즘 위키피디아 https://ko.wikipedia.org/wiki/A*_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
'공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] C++로 이해하는 DFS와 BFS (0) | 2025.04.03 |
|---|---|
| [알고리즘] 위상정렬(Topology Sort) (1) | 2024.10.11 |
| [알고리즘] LCS(Longest Common Subsequence) (0) | 2024.10.07 |
| [알고리즘] 백트래킹(Backtracking) (1) | 2024.09.14 |
| [알고리즘] 재귀란 무엇인가? (2) | 2024.09.14 |