
참고 : Introduction to Algorithms
☑️ C++로 이해하는 DFS와 BFS
DFS/BFS는 그래프(Graph)를 탐색하는 알고리즘을 의미한다. 그래프는 정점(Vertex)과 간선(Edge)을 통해 표현하는 자료구조를 말한다.
1️⃣ DFS (Depth First Search)
깊이 우선 탐색(Depth First Search)은 그래프를 탐색할 때, 깊이를 우선시하는 탐색 방법을 의미한다.
그래프를 탐색할 때, 정점 1을 시작으로 하위 정점들을 탐색해나간다. 탐색 우선 순위는 정점과 연결된 정점들을 탐색하고 연결된 정점이 없을 때, 이전으로 이동하여 남은 정점을 확인하고 탐색한다. 이러한 방법을 반복적으로 수행하며 최종적으로 모든 그래프의 정점을 탐색하게 된다.

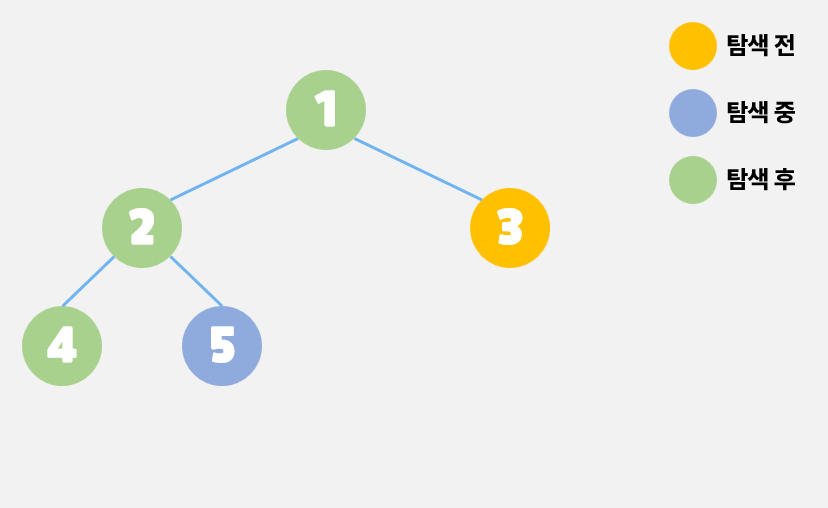
위 사진에서 DFS를 통해서 그래프를 탐색하게 된다면 정점 1 -> 정점 2 -> 정점 4의 순서로 탐색하게 된다. 정점 4는 탐색을 필요로 하는 연결된 정점이 없기 때문에 정점 2로 돌아가 정점 5를 탐색하게 된다. 이 과정을 통해 정점 3까지 탐색할 수 있다.
📌 C++로 구현한 DFS
void DFSVisit(int v) {
visited[v] = true;
for (int i = 0; i < adj[v].size(); i++) {
int adjacent = adj[v][i];
if (!visited[adjacent]) {
DFSVisit(adjacent);
}
}
}
void DFS(int startVertex) {
for (int i = 0; i < V; i++) {
visited[i] = false;
}
// 여기에서 0은 처음으로 시작하는 상위 정점
DFSVisit(0);
}정점을 방문 했는지를 확인하기 위해서 Boolean 타입의 변수를 같이 사용한다. DFS 함수에서 초기화를 진행하고 DFSVisit 함수에서 재귀 순회를 통해서 모든 정점을 탐색한다.
2️⃣ BFS (Breadth First Search)
너비 우선 탐색(Breadth First Search)은 탐색하는 정점과 인접한 정점을 우선 탐색하는 기법을 의미한다. 주로 정점 A부터 정점 Z까지 거리를 계산하는데에 사용될 수 있다. 주로 Queue를 사용해서 구현하는 방법이 일반적이다.
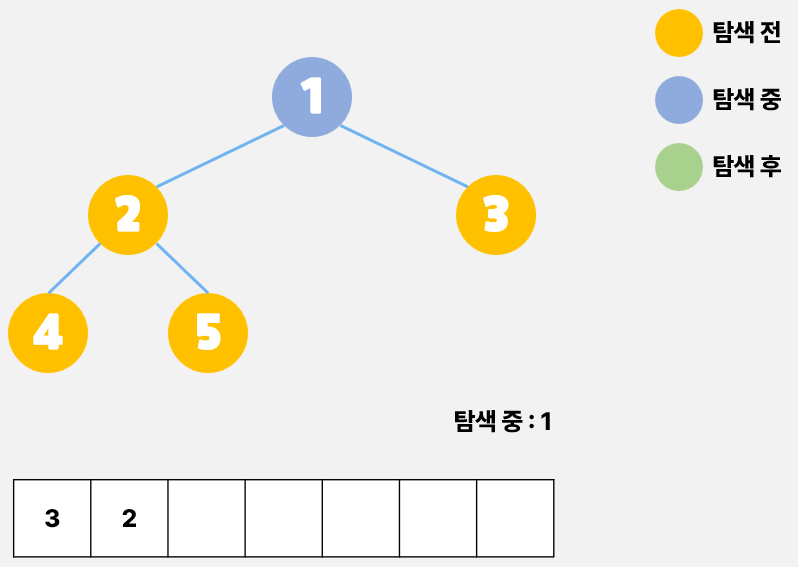
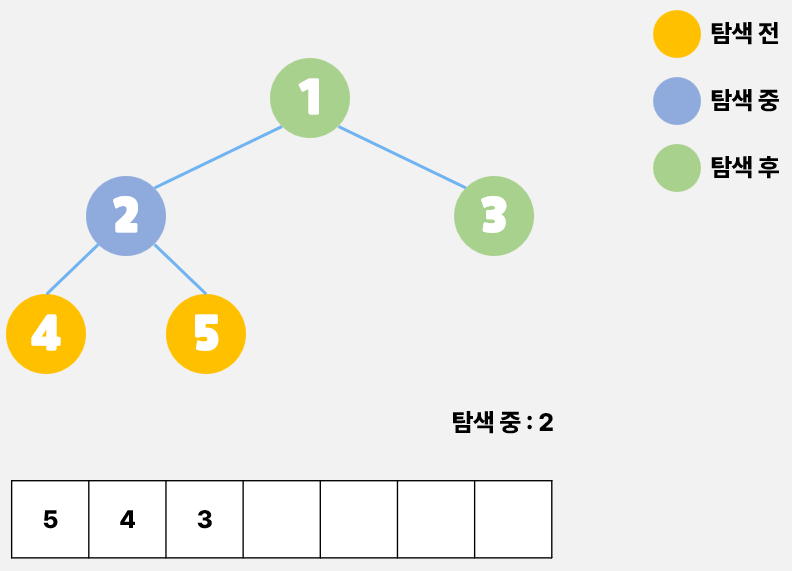
BFS는 탐색을 위해서 첫 노드를 Queue에 넣고 Queue가 빈 상태(Empty)가 될 때 까지 탐색하게 된다. 정점 1을 빼고 인접한 정점을 탐색한다. 정점 2와 정점 3이 나온다. 두 정점을 Queue에 추가하고 다시 지금까지의 과정을 반복해보자.
정점 2는 Queue의 최상단에 위치해있고 정점 2에서 인접한 정점 4와 정점 5를 다시 Queue에 추가한다. 다음 차례는 정점 3이지만, 인접한 노드가 없으므로 종료된다. 다음은 정점 4, 정점 5 순으로 반복하며 모든 그래프를 탐색하게 된다.
📌 C++로 구현한 BFS
void BFS(int startVertex) {
for (int i = 0; i < V; i++) {
visited[i] = false;
}
queue<int> q;
visited[startVertex] = true;
q.push(startVertex);
while (!q.empty()) {
int currentVertex = q.front();
q.pop();
for (int i = 0; i < adj[currentVertex].size(); i++) {
int adjacent = adj[currentVertex][i];
if (!visited[adjacent]) {
visited[adjacent] = true;
q.push(adjacent);
}
}
}
}'공부 > 알고리즘' 카테고리의 다른 글
| [알고리즘] C++로 이해하는 동적 프로그래밍 (0) | 2025.04.07 |
|---|---|
| [알고리즘] C++로 이해하는 검색 알고리즘(선형 검색, 이진 검색, 해시법 등) (0) | 2025.04.06 |
| [알고리즘] 위상정렬(Topology Sort) (1) | 2024.10.11 |
| [알고리즘] LCS(Longest Common Subsequence) (0) | 2024.10.07 |
| [알고리즘] 백트래킹(Backtracking) (1) | 2024.09.14 |